ОБЩИЕ ПРИНЦИПЫ РЕАЛИЗАЦИИ ВЗАИМООТНОШЕНИЙ В СИСТЕМЕ ОРГАНИЗМ — СРЕДА

Но отбросим печальные размышления и будем более оптимистичными. Попробуем привести взаимоотношения между метаболической и эпигенетической системами к общему, формализованному выражению, учитывая при этом, что в отличие от всех других специалистов биолог имеет дело со сложно организованной системой и его подход должен быть совершенно отличным от подхода инженера. Он не может изолировать даже условно часть, содержащую лишь несколько переменных, не нарушив общего поведения всей системы. Он не может произвести «линеаризацию», не утратив важнейших динамических свойств системы, ибо все явления в биологических системах, в том числе и результирующие (индивидуальный онтогенез), нелинейны. И наконец, он не может исследовать проблему регулирования так, как это делает инженер, т. е. пользуясь некоторыми известными критериями, искать сигнал обратной связи, обеспечивающей оптимальное поведение системы. Биолог не всегда может установить критерий оптимального протекания регуляторных или адаптивных процессов в клетке. Поэтому будем пока довольствоваться лишь некоторыми достаточно корректными математическими расчетами Гудвина.
Предположим, что концентрация метаболита M_i определяется концентрацией белка Y_i. Значит, Y_i представляет собой переменную, ограничивающую скорость синтеза M_i. Рассмотрим случай, когда M_i, являясь конечным продуктом реакционной цепи, поступает в общий метаболический фонд. В этом случае получается простейшая кинетическая схема, которую можно представить в виде уравнения:

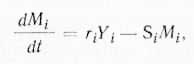
где S_i — константа скорости распада M_i которая имеет первый порядок; r_i — сложная константа, зависящая от констант скорости элементарных стадий, концентрации субстрата и константы Михоэлиса (K_m) для реакции, продуктом которой является М_i.
Вспомним, что Y_i и M_i принадлежат к разным системам: первая — к эпигенетической, вторая — к метаболической. Поэтому различия между изменениями их скоростей очень велики (вспомним также идею о временных релаксациях). Следовательно, можно считать, что М_i находится в стационарном состоянии во время Y_i, т. е. можно написать:

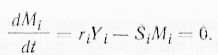
Динамическое поведение метаболических фондов в клетке, где работают колебательные регуляторные механизмы, осложняется тем, что размеры этих фондов сами колеблются. Это следует из уравнения, показывающего, что при рассмотрении отрезков времени, характерных для эпигенетической системы, M_i ведет себя но существу так же, как и Y_i. На более коротких отрезках времени поведение M_i будет определяться также взаимодействиями внутри метаболической системы, но они могут рассматриваться как «шумы» по отношению к эпигенетическим процессам, если принять предположение о наличии существенной разницы в величинах релаксаций. Однако так называемый метаболический шум отнюдь не помеха, а основа проявления релаксационных свойств эпигенетической системы. В связи с тем что и метаболические, и эпигенетические процессы имеют колебательную природу, естественно, что используемая при этом свободная энергия G также носит колебательный характер и соответственно названа Гудвином таландической.
Так, можно представить, что некоторое число соединений V не изолировано от остальных компонентов клетки и обменивается с ними таландической энергией n — V. Если я очень велико, то для подавляющего большинства компонентов канонического ансамбля G_i будет довольно близко к каноническому среднему Ḡ.